• 软引用

内存敏感缓存：当内存不足时才会被回收

比弱引用”强”：JVM会尽量保留软引用对象

1
2
3

// 创建软引用
SoftReference<byte[]> softRef = 
    new SoftReference<>(new byte[1024 * 1024]); // 1MB

• 弱引用

短期缓存：只要发生GC就会被回收

不会阻止回收：比软引用更脆弱

1
2
3

// 创建弱引用
WeakReference<Object> weakRef = 
    new WeakReference<>(new Object());

• 虚引用

内存敏感缓存：当内存不足时才会被回收

比弱引用”强”：JVM会尽量保留软引用对象

1
2
3

// 创建软引用
SoftReference<byte[]> softRef = 
    new SoftReference<>(new byte[1024 * 1024]); // 1MB

2PC、TCC、SAGA、本地消息表的原理和优缺点分别是什么？在实际项目中如何选择合适的分布式事务方案？

SAGA

将分布式事务拆分为一系列本地事务的有序执行链，每个本地事务都有对应的补偿事务：

正向执行

按顺序执行每个本地事务 T1, T2, …, Tn。
如果所有本地事务都执行成功，事务提交。

反向补偿

如果某个本地事务 Ti 执行失败，按逆序执行补偿事务 Ci-1, Ci-2, …, C1。
补偿事务的作用是撤销对应正向本地事务的执行结果，恢复到事务执行前的状态。

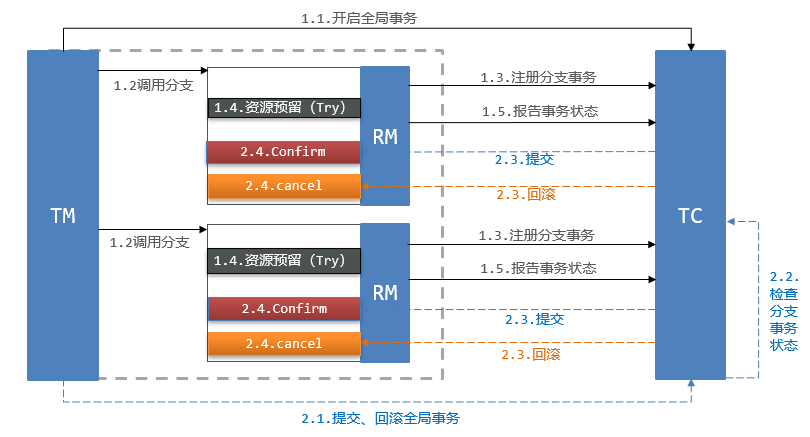
TCC（Try-Confirm-Cancel，补偿事务）

TCC 是一种业务侵入式的分布式事务方案，将每个业务操作拆分为三个独立的方法，由业务代码实现：

1.Try 阶段

尝试执行业务操作，预留资源（如冻结资金、锁定库存），保证操作的幂等性。

此阶段只做资源检查和预留，不执行最终业务逻辑。

2.Confirm 阶段

确认执行业务操作，使用预留的资源完成最终逻辑。

只有当所有参与者的 Try 阶段都成功时，才会执行 Confirm 阶段。

3.Cancel 阶段

取消执行业务操作，释放预留的资源。

如果任何一个参与者的 Try 阶段失败，会执行所有参与者的 Cancel 阶段。

幂等、空回滚、悬挂？

幂等性就是无论接口调用多少次，返回的结果应该具有一致性。

空回滚（try没执行就cancel）：当某分支事务的try阶段阻塞时，可能导致全局事务超时而触发二阶段的cancel操作。在未执行try操作时先执行了cancel操作，这时cancel不能做回滚，就是空回滚。

业务悬挂（cancel之后try）：对于已经空回滚的业务，如果以后继续执行try，就永远不可能confirm或cancel

• 资金业务的具体例子：

为了实现空回滚、防止业务悬挂,记录冻结金额的同时,记录当前事务id和执行状态

1
2
3
4
5
6
7

CREATE TABLE `account_freeze_tbl` (
  `xid` varchar(128) NOT NULL COMMENT '事务id',
  `user_id` varchar(255) DEFAULT NULL COMMENT '用户id',
  `freeze_money` int(11) unsigned DEFAULT '0' COMMENT '冻结金额',
  `state` int(1) DEFAULT NULL COMMENT '事务状态，0:try，1:confirm，2:cancel',
  PRIMARY KEY (`xid`) USING BTREE
) ENGINE=InnoDB DEFAULT CHARSET=utf8 ROW_FORMAT=COMPACT;

1.Try业务

记录冻结金额和事务状态0到account_freeze表

扣减account表可用金额

2.Confirm业务

根据xid删除account_freeze表的冻结记录(因为如果一个事务confirm那么记录就没有意义了)

3.Cancel业务

修改account_freeze表，冻结金额为0，state为2

修改account表，恢复可用金额

• 如何判断是否空回滚:

cancel业务中，根据xid查询account_freeze，如果为null则说明try还没做，需要空回滚

• 如何避免业务悬挂:

try业务中，根据xid查询account_freeze ，如果存在金额=0/state=2则证明Cancel已经执行，拒绝执行try业务

TCC vs 2PC

TCC只需要处理业务异常情况，异常处理相对简单。 2PC适用于对事务一致性要求较高的场景，例如银行转账等，需要保证数据致性和完整性。 而TCC适用于对事务一致性要求不那么高的场景，例如电商库存扣减等，需要保证数据最终一致性即可。

本地消息表

写本地消息+状态，然后链式流转。

double check lock 懒汉模式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

public class DCLSingleton {
    // 使用 volatile 关键字，防止指令重排
    private static volatile DCLSingleton instance;

    private DCLSingleton() {
        System.out.println("DCLSingleton 被实例化");
    }

    public static DCLSingleton getInstance() {
        // 第一次检查：如果实例已存在，直接返回
        if (instance == null) {
            // 加锁
            synchronized (DCLSingleton.class) {
                // 第二次检查：防止多个线程同时进入第一个 if 后重复创建实例
                if (instance == null) {
                    instance = new DCLSingleton();
                }
            }
        }
        return instance;
    }
}

饿汉模式

1
2
3
4
5
6
7
8
9
10
11
12

public class EagerSingleton {
    // 在类加载时就初始化实例
    private static final EagerSingleton INSTANCE = new EagerSingleton();

    private EagerSingleton() {
        System.out.println("EagerSingleton 被实例化");
    }

    public static EagerSingleton getInstance() {
        return INSTANCE;
    }
}

enum

1
2
3
4
5
6
7
8
9
10
11

public enum EnumSingleton {
    INSTANCE;

    EnumSingleton() {
        System.out.println("EnumSingleton 被实例化");
    }

    public void doSomething() {
        System.out.println("枚举单例执行方法");
    }
}

用于构建锁和同步器。它为实现复杂的线程同步机制提供了基础支持。

AQS 解决了开发者在实现同步器时的复杂性问题。它提供了一个通用框架，用于实现各种同步器，例如 可重入锁（ReentrantLock）、信号量（Semaphore）和 倒计时器（CountDownLatch）。通过封装底层的线程同步机制，AQS 将复杂的线程管理逻辑隐藏起来，使开发者只需专注于具体的同步逻辑。

AQS 内部大量使用了 CAS 操作。AQS 内部通过队列来存储等待的线程节点。由于队列是共享资源，在多线程场景下，需要保证队列的同步访问。AQS 内部通过 CAS 操作来控制队列的同步访问，CAS 操作主要用于 控制队列初始化、线程节点入队 两个操作的并发安全。虽然利用 CAS 控制并发安全可以保证比较好的性能，但同时会带来比较高的编码复杂度。

AQS 为构建锁和同步器提供了一些通用功能的实现。因此，使用 AQS 能简单且高效地构造出应用广泛的大量的同步器，比如我们提到的 ReentrantLock，Semaphore，其他的诸如 ReentrantReadWriteLock，SynchronousQueue等等皆是基于 AQS 的。

JAVA 1.6 之后的改进

• 可重入锁

• 偏向锁

共享资源首次被访问时，JVM会对该共享资源对象做一些设置，比如将对象头中是否偏向锁标志位置为1，对象头中的线程ID设置为当前线程ID（注意：这里是操作系统的线程ID），后续当前线程再次访问这个共享资源时，会根据偏向锁标识跟线程ID进行比对是否相同，比对成功则直接获取到锁，进入临界区域（就是被锁保护，线程间只能串行访问的代码），这也是synchronized锁的可重入功能。

• 轻量级锁

当多个线程同时申请共享资源锁的访问时，这就产生了竞争，JVM会先尝试使用轻量级锁，以CAS方式来获取锁（一般就是自旋加锁，不阻塞线程采用循环等待的方式），成功则获取到锁，状态为轻量级锁，失败（达到一定的自旋次数还未成功）则锁升级到重量级锁。

• 重量级锁

如果共享资源锁已经被某个线程持有，此时是偏向锁状态，未释放锁前，再有其他线程来竞争时，则会升级到重量级锁，另外轻量级锁状态多线程竞争锁时，也会升级到重量级锁，重量级锁由操作系统来实现，所以性能消耗相对较高。

这4种级别的锁，在获取时性能消耗：重量级锁 > 轻量级锁 > 偏向锁 > 无锁。

为什么偏向锁被废弃？

偏向锁是 HotSpot 虚拟机的一项优化技术，可以提升单线程对同步代码块的访问性能。受益于偏向锁的应用程序通常使用了早期的 Java 集合 API，例如 HashTable、Vector，在这些集合类中通过 synchronized 来控制同步，这样在单线程频繁访问时，通过偏向锁会减少同步开销。随着 JDK 的发展，出现了 ConcurrentHashMap 高性能的集合类，在集合类内部进行了许多性能优化，此时偏向锁带来的性能收益就不明显了。偏向锁仅仅在单线程访问同步代码块的场景中可以获得性能收益。如果存在多线程竞争，就需要撤销偏向锁 ，这个操作的性能开销是比较昂贵的。偏向锁的撤销需要等待进入到全局安全点（safe point），该状态下所有线程都是暂停的，此时去检查线程状态并进行偏向锁的撤销。

类加载过程

加载：导入方法区，在内存中生成一个代表该类的 Class 对象，作为方法区这些数据的访问入口。

验证：确保 Class 文件的字节流中包含的信息符合《Java 虚拟机规范》的全部约束要求，保证这些信息被当作代码运行后不会危害虚拟机自身的安全。

准备：正式为类变量分配内存并设置类变量初始值的阶段，这些内存都将在方法区中分配。

解析：符号引用验证发生在类加载过程中的解析阶段，具体点说是 JVM 将符号引用转化为直接引用的时候（解析阶段会介绍符号引用和直接引用）。解析动作主要针对类或接口、字段、类方法、接口方法、方法类型、方法句柄和调用限定符 7 类符号引用进行。

初始化：执行初始化方法 ()方法的过程，是类加载的最后一步，这一步 JVM 才开始真正执行类中定义的 Java 程序代码(字节码)。

卸载：需要满足 3 个要求

（1）该类的所有的实例对象都已被 GC，也就是说堆不存在该类的实例对象。

（2）该类没有在其他任何地方被引用

（3）该类的类加载器的实例已被 GC

类加载器

BootstrapClassLoader(启动类加载器)：最顶层的加载类，由 C++实现，通常表示为 null，并且没有父级，主要用来加载 JDK 内部的核心类库（ %JAVA_HOME%/lib目录下的 rt.jar、resources.jar、charsets.jar等 jar 包和类）以及被 -Xbootclasspath参数指定的路径下的所有类。

ExtensionClassLoader(扩展类加载器)：主要负责加载 %JRE_HOME%/lib/ext 目录下的 jar 包和类以及被 java.ext.dirs 系统变量所指定的路径下的所有类。【这些类属于 Java 标准库的扩展部分，例如加密、国际化等功能】

AppClassLoader(应用程序类加载器)：面向我们用户的加载器，负责加载当前应用 classpath 下的所有 jar 包和类。【运行一个 Java 程序时，java 命令会指定 classpath】

CustomClassLoader：用户还可以加入自定义的类加载器来进行拓展，以满足自己的特殊需求。就比如说，我们可以对 Java 类的字节码（ .class 文件）进行加密，加载时再利用自定义的类加载器对其解密。

rt.jar：rt 代表“RunTime”，rt.jar是 Java 基础类库，包含 Java doc 里面看到的所有的类的类文件。也就是说，我们常用内置库 java.xxx.都在里面，比如java.util.、java.io.、java.nio.、java.lang.、java.sql.、java.math.*。

双亲委派模型

双亲委派模型是 Java 类加载机制的重要组成部分，它通过委派父加载器优先加载类的方式，实现了两个关键的安全目标：避免类的重复加载和防止核心 API 被篡改。

即使攻击者绕过了双亲委派模型，Java 仍然具备更底层的安全机制来保护核心类库。ClassLoader 的 preDefineClass 方法会在定义类之前进行类名校验。任何以 “java.” 开头的类名都会触发 SecurityException，阻止恶意代码定义或加载伪造的核心类。

打破双亲委派模型方法

• 打破低级别类加载器load高级别

重写 loadClass()方法之后，我们就可以改变传统双亲委派模型的执行流程。例如，子类加载器可以在委派给父类加载器之前，先自己尝试加载这个类，或者在父类加载器返回之后，再尝试从其他地方加载这个类。具体的规则由我们自己实现，根据项目需求定制化。

• 想让高级别类加载器load低级别

使用线程上下文类加载器，线程上下文类加载器的原理是将一个类加载器保存在线程私有数据里，跟线程绑定，然后在需要的时候取出来使用。这个类加载器通常是由应用程序或者容器（如 Tomcat）设置的。

• 可重入，内部有计数器 ++ — 到 0 释放锁

• 可以公平也可以非公平锁

• 悲观锁

• 可以tryLock(long timeout, TimeUnit unit) 方法，允许线程在指定时间内尝试获取锁，如果超时则返回 false。

• 中断响应，允许线程在等待锁的过程中响应中断。

获取锁流程

非公平锁：基于CAS获取锁，拿不到就去AQS队列等待。

AQS 队列

AQS 使用一个 双向链表 来管理等待线程，每个节点是一个 Node 对象：

prev：前驱节点。

next：后继节点。

thread：等待的线程。

waitStatus：节点状态（如 SIGNAL、CANCELLED 等）。

当线程获取锁失败时，会被加入队列尾部，并通过 LockSupport.park() 阻塞。当锁释放时，会唤醒队列头部的线程。

可以解决循环依赖的场景

单例 Bean（非单例不行） + 基于字段注入（@Autowired） 或 setter 注入。

构造器注入无法解决循环依赖，因为构造器注入在实例化时就需要依赖对象，此时依赖对象还没创建。

解决循环依赖发的办法

1.@Lazy

1
2
3
4
5
6
7
8
9
10
11
12

@Component
public class A {
    @Autowired
    @Lazy
    private B b;
}

@Component
public class B {
    @Autowired
    private A a;
}

@Lazy 会延迟初始化 B，从而打破循环。

2.如果使用构造器注入出现循环依赖，可以改为 setter 注入。

三级缓存方案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

┌─────────────────────────────────────────────────────────────────────┐
│ Spring 容器启动                                                    │
└─────────────────────────────────────────────────────────────────────┘
            │
            ▼
┌─────────────────────────────────────────────────────────────────────┐
│ 创建 Bean A                                                        │
│   1. 检查一级缓存 singletonObjects → 没有 A                         │
│   2. 检查二级缓存 earlySingletonObjects → 没有 A                    │
│   3. 检查三级缓存 singletonFactories → 没有 A                       │
│   4. 将 A 标记为正在创建（added to singletonsCurrentlyInCreation）  │
│   5. 创建 A 的 ObjectFactory 并放入三级缓存 singletonFactories       │
│   6. 实例化 A（调用构造方法）                                        │
│   7. 填充 A 的属性（发现需要注入 B）                                 │
└─────────────────────────────────────────────────────────────────────┘
            │
            ▼
┌─────────────────────────────────────────────────────────────────────┐
│ 创建 Bean B                                                        │
│   1. 检查一级缓存 singletonObjects → 没有 B                         │
│   2. 检查二级缓存 earlySingletonObjects → 没有 B                    │
│   3. 检查三级缓存 singletonFactories → 没有 B                       │
│   4. 将 B 标记为正在创建（added to singletonsCurrentlyInCreation）  │
│   5. 创建 B 的 ObjectFactory 并放入三级缓存 singletonFactories       │
│   6. 实例化 B（调用构造方法）                                        │
│   7. 填充 B 的属性（发现需要注入 A）                                 │
└─────────────────────────────────────────────────────────────────────┘
            │
            ▼
┌─────────────────────────────────────────────────────────────────────┐
│ 注入 A 到 B 时解决循环依赖                                         │
│   1. 检查一级缓存 singletonObjects → 没有 A                         │
│   2. 检查二级缓存 earlySingletonObjects → 没有 A                    │
│   3. 检查三级缓存 singletonFactories → 有 A 的 ObjectFactory        │
│   4. 通过 ObjectFactory 获取 A 的半成品（可能是代理对象）            │
│   5. 将 A 的半成品放入二级缓存 earlySingletonObjects                │
│   6. 从三级缓存 singletonFactories 移除 A 的 ObjectFactory           │
│   7. 将 A 的半成品注入到 B                                          │
└─────────────────────────────────────────────────────────────────────┘
            │
            ▼
┌─────────────────────────────────────────────────────────────────────┐
│ B 创建完成                                                         │
│   1. 将 B 放入一级缓存 singletonObjects                            │
│   2. 从二级缓存 earlySingletonObjects 移除 B（如果有）              │
│   3. 从三级缓存 singletonFactories 移除 B（如果有）                 │
└─────────────────────────────────────────────────────────────────────┘
            │
            ▼
┌─────────────────────────────────────────────────────────────────────┐
│ 继续创建 A                                                         │
│   1. 将 B 注入到 A                                                  │
│   2. A 创建完成                                                    │
│   3. 将 A 放入一级缓存 singletonObjects                            │
│   4. 从二级缓存 earlySingletonObjects 移除 A                        │
│   5. 从三级缓存 singletonFactories 移除 A                           │
└─────────────────────────────────────────────────────────────────────┘

常用初始化模块执行顺序

构造函数 > @Autowired > @PostConstruct > init函数

bean的生命周期「实例化 → 属性填充 → 初始化 → 使用 → 销毁」

1.实例化

Spring 首先实例化一个 Bean，并为其分配内存空间。这个阶段就是通过 Spring 的 ApplicationContext 或 BeanFactory 根据 Bean 定义的类信息（通过 XML 配置或注解）创建 Bean 对象的过程。

Spring 通过反射机制创建 Bean 的实例（调用构造方法）

2.属性赋值（依赖注入）

实例化完成后，Spring 会通过依赖注入（DI）机制为 Bean 设置属性。这个过程确保了所有依赖项（无论是通过构造器注入还是通过 setter 注入）都会被自动注入。
依赖注入的方式有多种，其中最常见的是使用 @Autowired 注解或者通过 XML 配置来完成。

3.初始化

在属性赋值后，Spring 会调用一些初始化方法来完成额外的配置。初始化阶段非常关键，因为它通常依赖于前面注入的属性值，确保在执行相关操作时，属性已经正确赋值。
初始化过程包括以下几个步骤：

前置初始化方法：可以通过 @PostConstruct 注解或者实现 InitializingBean 接口的 afterPropertiesSet() 方法来定义。
初始化方法执行：开发者可以通过在 Bean 配置文件中指定自定义的初始化方法（比如 init-method）。

4.使用

5.销毁

• 代码调用的时候初始化

什么时候事务无法传递？

1.AOP代理失败

如果在 同一个类内部 直接调用带有 @Transactional 注解的方法，调用不会经过代理，事务失效。

1
2
3
4
5
6
7
8
9
10
11
12
13

@Service
public class UserService {

    public void updateUser() {
        // 直接调用本类的事务方法，事务失效
        doUpdate();
    }

    @Transactional
    public void doUpdate() {
        // 事务逻辑
    }
}

• 解决方法：

1.通过 Spring 容器获取代理对象（如 self = applicationContext.getBean(UserService.class)）。

2.拆分到不同的类中，让调用走代理。

2.异常类型不匹配

Spring 默认只在 运行时异常（RuntimeException） 或 Error 时回滚事务，受检异常（Checked Exception） 默认不会回滚。

1
2
3
4
5

@Transactional
public void updateUser() throws Exception {
    // 抛出受检异常，事务不会回滚
    throw new Exception("出错了");
}

• 解决方案：

显式指定回滚异常类型：

1

@Transactional(rollbackFor = Exception.class)

3.事务方法被声明为 static 或 final

Spring 事务代理需要生成子类（CGLIB）或实现接口（JDK 动态代理）。如果方法是 static 或 final，代理无法覆盖，事务失效。

1
2
3
4

@Transactional
public final void updateUser() {
    // 事务失效
}

4.事务方法不是 public

Spring 事务代理只对 public 方法 生效，private、protected 或默认访问权限的方法不会被代理。

5.多线程环境下事务失效

Spring 事务是基于 ThreadLocal 管理的，如果在事务方法中开启新线程，新线程无法继承事务上下文，事务失效。

1
2
3
4
5
6

@Transactional
public void updateUser() {
    new Thread(() -> {
        // 新线程中的事务逻辑，事务失效
    }).start();
}

6.数据源或事务管理器配置错误

数据源未被 Spring 事务管理器管理。

事务管理器配置的数据源与实际使用的数据源不一致。

1
2
3
4

@Bean
public PlatformTransactionManager transactionManager(DataSource dataSource) {
    return new DataSourceTransactionManager(dataSource);
}