2025-12-27

JVM垃圾回收算法

知识概念

CMS垃圾回收

回收步骤：

年轻代使用复制算法，老年代使用标记-清除算法。

老年代GC触发条件：CMS 不会等到老年代完全满了才进行回收，而是当老年代使用达到一定阈值时（默认 92%）开始回收，以避免长时间的 Full GC。

标记策略 - 增量更新

在并发标记过程中，当发现一个原本未被标记为存活的对象，因为某个应用程序线程执行了写操作而使得其被一个已标记的存活对象引用时，并不会立即将这个原本未标记的对象标记为存活，而是将这个引用关系变化记录下来，等待重新标记阶段再根据这些记录来更新标记情况，确保该对象能被正确标记为存活。

CMS使用插入写屏障

新增黑色到白色的引用，JVM就会通过写屏障，将黑色变成灰色

CMS 也有卡表

在CMS中，写屏障主要用于记录跨代引用（即老年代对象引用新生代对象或反之）的变化，并将这些变化信息反映到卡表中。

卡表本质是bit数组，帮助定位需要重新扫描的老年代区域。

CMS缺点：

内存碎片问题：由于 CMS 是标记-清除回收器，不会整理内存，老年代内存中会产生碎片，这可能导致 Full GC。

并发模式失败：如果老年代在回收过程中无法及时腾出足够空间，可能会发生“Concurrent Mode Failure”，这会退回到单线程的 Serial Old GC，导致长时间暂停。

较高 CPU 消耗：CMS 在回收时需要额外的 CPU 资源，可能对 CPU 密集型应用有较大影响。

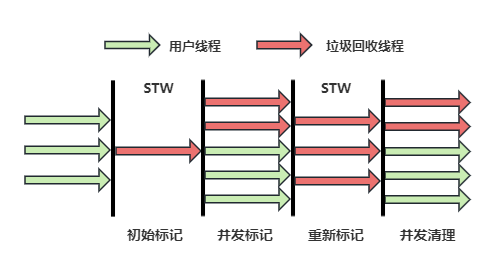
CMS_STW

浮动垃圾：CMS垃圾回收器在并发标记和并发清理阶段由于用户线程并未停止，该阶段可能会产生浮动垃圾，无法在本次被回收，只能等到下一次垃圾回收。

G1（Garbage First GC）

参考链接：https://mp.weixin.qq.com/s/RqLSu8VNcvQRMh0D-QA9Bw

分区堆模型：G1 将堆分成多个大小相等的区域（Region），不同区域可能属于年轻代或老年代。通过收集垃圾最多的区域进行复制回收，因此称为“Garbage First”。

混合回收：G1 能够同时回收年轻代和老年代的内存，避免了 Full GC 的大范围内存整理。

暂停时间可控：G1 可以根据设置的最大暂停时间目标（默认 200ms），智能选择要回收的区域，来控制 GC 的影响。

生产环境中，G1 最稳定的堆内存范围是8GB ~ 128GB；少数优化到位的场景（如高 CPU 核心、低对象分配速率）可到 256GB，但超过 256GB 后，G1 很难维持低延迟

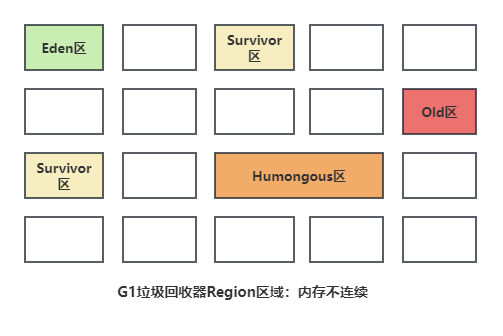
区块划分

Eden区、Survivor区、Old区和Humongous区（存放大对象，老年代的一部分）

区域Region的内存大小默认是通过整个堆内存大小除以2048得到的，例如整个堆内存为4G，则Region = 4G / 2048 = 2M，同时也支持通过JVM参数指定Region的内存大小。

upload successful

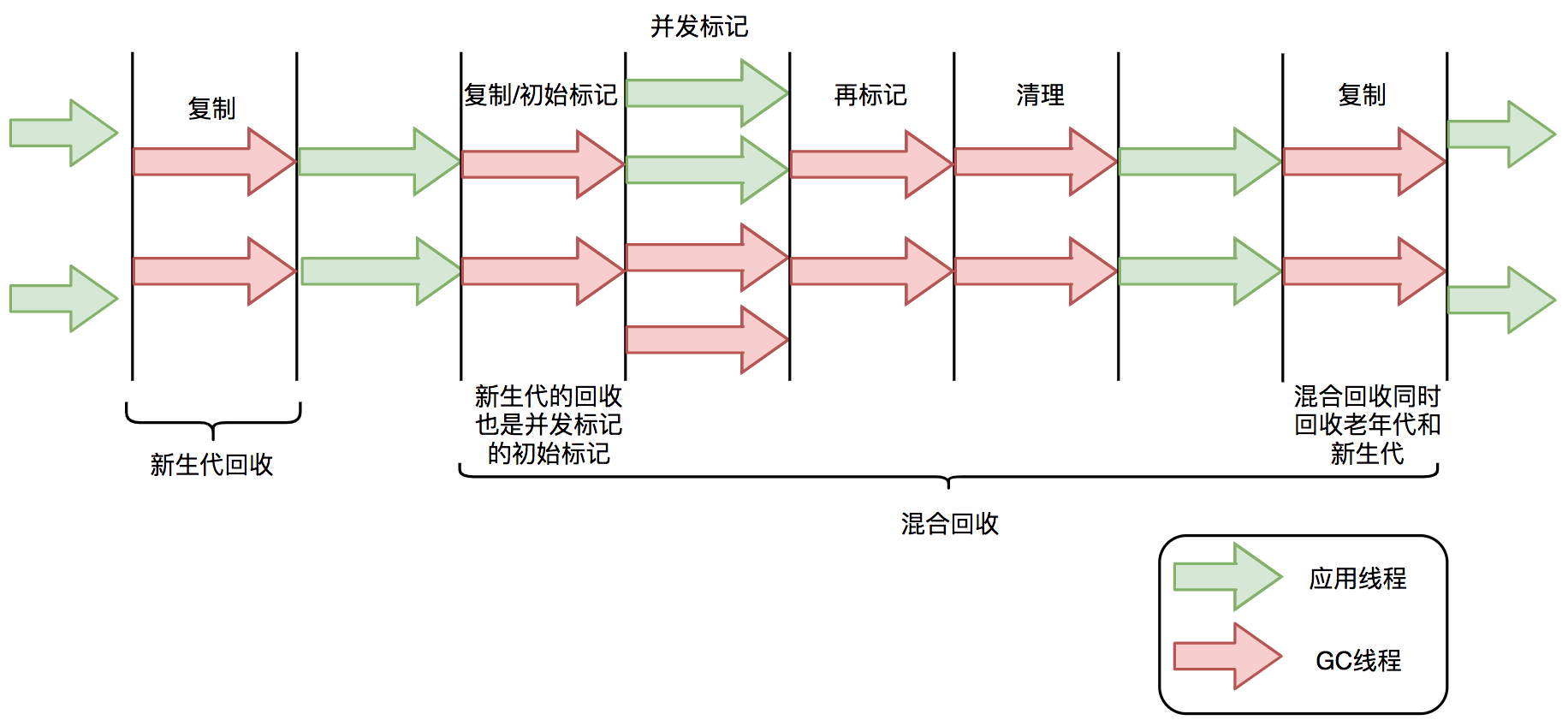
阶段划分

年轻代回收（Young GC）阶段：

当Eden区被填满或者达到了某个条件（例如，G1认为回收这些区域的收益较高）时，就会触发一次年轻代回收。

年轻代回收的过程中，存活的对象会从Eden区和Survivor区复制到另一个Survivor区或者直接晋升到老年代。

这个过程通常是Stop-The-World（STW）的，即在回收过程中，应用程序的其他线程会被暂停。

混合回收（Mixed GC）阶段：

当老年代的占用率达到了一定阈值（由-XX:InitiatingHeapOccupancyPercent参数控制，默认值为45%），G1会启动混合回收阶段。

在这个阶段，G1不仅回收年轻代，还会回收一部分老年代的区域，这些区域被认为含有较多垃圾。

混合回收也是STW的，但G1会尝试在用户指定的停顿时间目标内完成。

回收技术

G1垃圾回收器年轻代回收时，采用了三种关键技术，分别是记忆集、卡表和写屏障。

如果年轻代的对象被老年代的对象引用了，应该如何识别出来呢？

记忆集和卡表实现

当某个卡页中的对象引用自己Region区域的对象时，会将老年代的卡表对应编号位置的字节修改为1，为1的字节被称之为脏卡。

在Young GC回收年轻代对象时，会将记忆集中的对象也加入到GC Root中，有效避免年轻代的对象被错误的回收。

G1卡表和CMS卡表有啥区别？

G1卡表维护范围：覆盖整个堆（包括年轻代和老年代分区）。CMS只是老年代。

G1卡表维护信息：对每张卡，不仅标记是否脏，还关联对应的 Region 信息，方便定位影响的区域。

SATB：

核心思想是：在标记过程的起始阶段捕捉一个对象的快照，并基于这个快照来进行后续的标记工作。

在标记阶段开始时，G1垃圾收集器会创建一个当前所有对象的快照。

在这个快照之后新生成的对象，由于它们尚未被任何旧对象引用，因此它们会被直接标记为黑色，表示它们是活跃的，不应该被回收。

为了处理在标记过程中可能发生的对象引用变化，G1采用了前置写屏障技术。

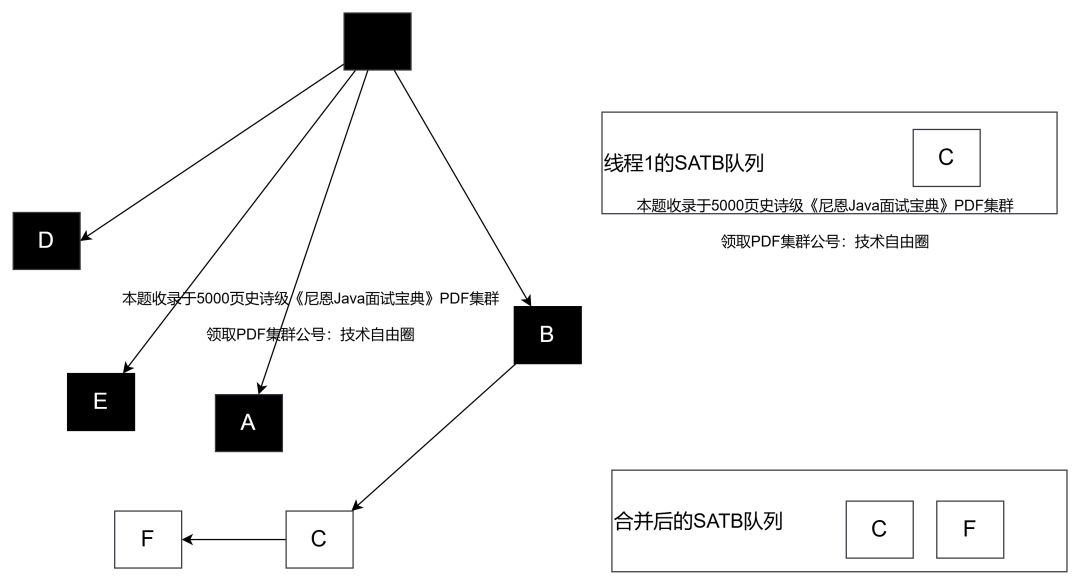
前置写屏障技术会在引用赋值操作（如B.c = null）之前被触发，将即将被改变引用的对象（在这个例子中是C）放入SATB待处理队列中。

每个线程都有自己的SATB队列，但最终这些队列会被汇总到一个全局的SATB队列中。

upload successful

写屏障：

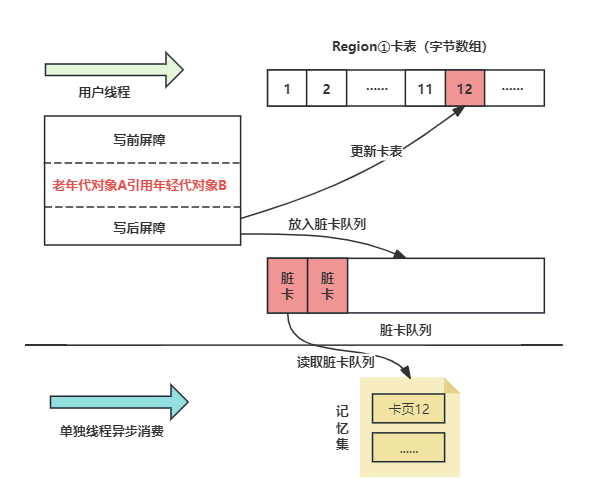
更新卡表状态的底层采用了写屏障技术（具体为写后屏障），当执行对象引用相关的代码时，会在其代码前后插入对应的指令，判断到老年代对象引用年轻代对象时，会更改卡表中对应的字节为脏卡，同时会将脏卡放入到一个脏卡队列中，JVM会通过单独的线程，定期读取脏卡队列中的数据，更新记忆集。

upload successful

优点：

适用于大堆内存：G1 尤其适合大堆内存（通常超过 6GB）环境，能够有效处理较大的老年代回收。

避免 Full GC：通过区域化内存管理和并行收集，G1 几乎避免了传统的 Full GC 停顿。

碎片整理：G1 在回收时会进行内存整理，减少了内存碎片问题。

提前触发回收（少量多次），每次垃圾回收时间短。

G1_STW

浮动垃圾：SATB基于初始快照进行标记，因此在本轮垃圾回收过程中，可能会将一些实际上应该被回收的不存活对象错误地标记为存活对象。这些错误标记的对象被称为“浮动垃圾”。这些浮动垃圾只能下一次的时候回收。

问题排查：G1在执行Full GC时，会在GC日志中记录相关信息，如[Full GC (Allocation Failure)]，表示由于分配失败触发了Full GC。
怎么实现的预测回收STW？

如果目标延迟是 50ms，G1 会计算 “回收多少个 Region 能在 50ms 内完成”，只回收这部分，剩下的留到下一次 GC 处理。

如果某次 GC 实际停顿超过了目标值，模型会在下一次自动减少回收的 Region 数量；如果远低于目标值，会适当增加，平衡延迟和吞吐量。

ZGC

超低延迟：ZGC 是一种面向超低延迟设计的垃圾回收器，旨在将垃圾回收停顿时间控制在 10ms 以内。

堆内存极大：ZGC 支持非常大的堆内存（TB 级别），这使得它在处理大规模内存应用时有很大的优势。

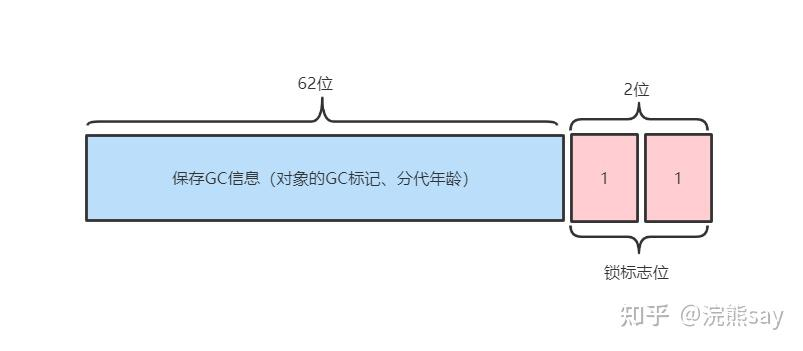
1.着色指针（Colored Pointers）

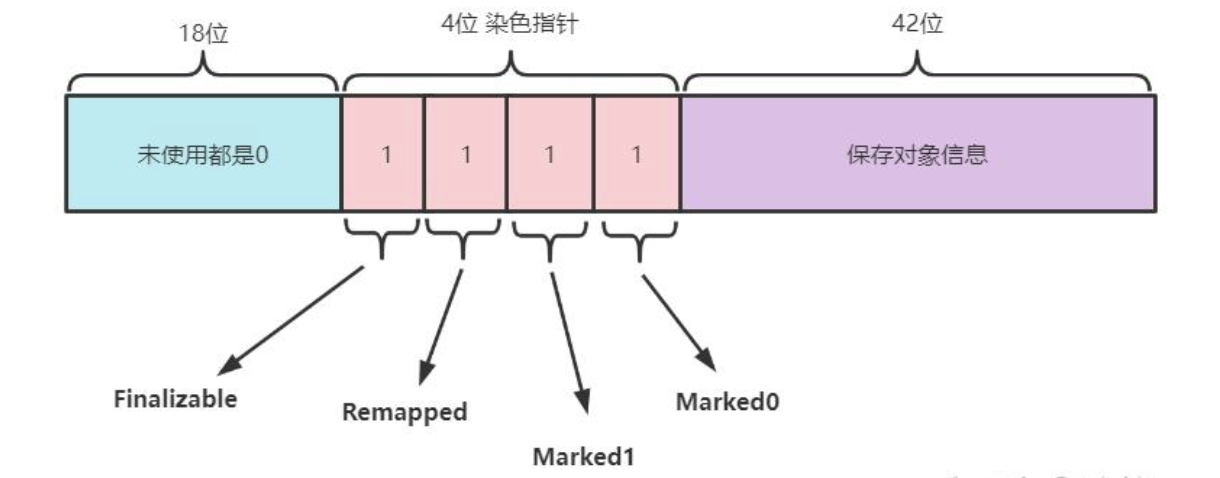
upload successful

原理：利用 64 位指针的高几位空闲位（不同 CPU 架构空闲位不同，如 x86-64 保留 18 位）存储标记信息，包括：高18位都是0暂未使用，剩余的46位实际上是能支持64TB的内存的，但是目前来说计算机内存空间还没这么大。剩余的46位中，高4位用来保存了4个标志位，低42位置才是用来保存对象的指针，所以ZGC最大可以管理的内存不超过4TB。

Marked0/Marked1：三色标记对象是否存活（用于并发标记）；

Remapped：标记对象是否已完成重定位（用于并发重定位）。

Finalizable：是否需要通过 finalize 方法来访问到（Finalizable）等信息。

优势：
无需修改对象头，减少内存占用；

指针本身携带状态，GC 阶段无需扫描整个堆，大幅提升效率；

支持并发重定位（对象移动时，应用线程可同时访问旧指针，由读屏障透明转发到新地址）。

upload successful

2.读屏障（Load Barrier）

ZGC 仅在应用线程读取对象指针时插入读屏障，核心作用是：

指针验证：检查指针的标记位是否合法；

指针转发：若对象已被移动，自动将旧指针转发到新地址；

并发标记辅助：在标记阶段，协助标记对象的可达性。

读屏障的性能开销极低（实测约 1%~3%），远小于传统 GC 的写屏障。

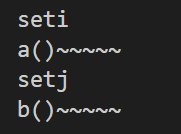
在从堆读取引用时介入：

1	Object o = obj.fieldA; // 触发读屏障

当对象被移动时，屏障自动修正指针，实现指针自愈。

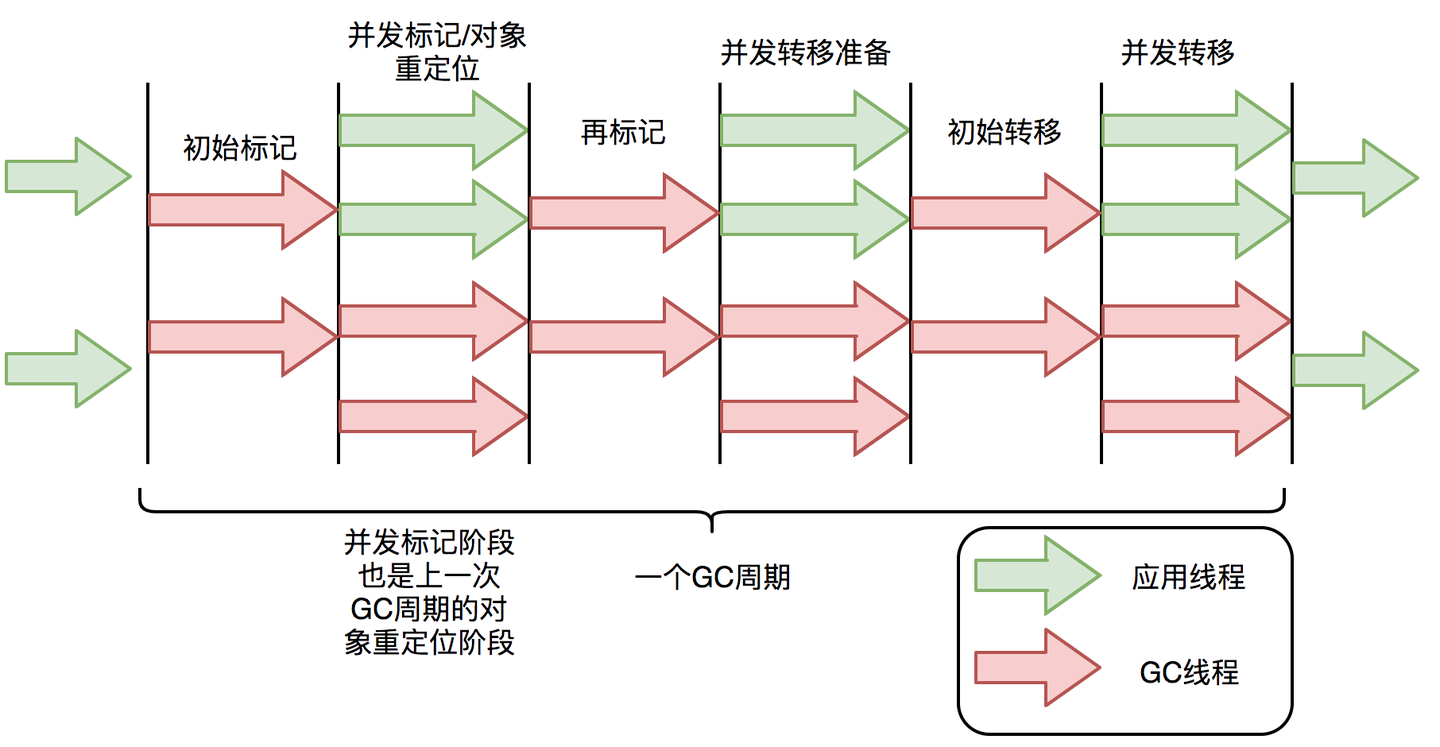
回收流程

1.初始标记（Initial Mark）- STW

目标：标记 GC Root 直接引用的对象。

特点：停顿时间微秒级，几乎可以忽略，通常与线程的 safepoint 重合。

2.并发标记（Concurrent Mark）- 并发

目标：从初始标记的对象出发，遍历整个对象图，标记所有存活对象（通过着色指针的 Marked0/Marked1 位）。

特点：与应用线程并发执行，无停顿；标记过程中，新分配的对象自动标记为存活。

3.重定位（Relocation）- 并发 + 极短 STW

这是 ZGC 实现低延迟的核心阶段，分为三步：

重定位选择（Concurrent Relocation Selection）：并发选择需要回收的 Region（垃圾比例高的 Region）；

重定位准备（Concurrent Relocation Preparation）：准备重定位的 Region，标记为 “正在重定位”；

并发重定位（Concurrent Relocation）：将存活对象移动到新的 Region，同时通过读屏障让应用线程透明访问新地址；

最终重定位（Final Relocation）：极短 STW，处理极少数未转发的旧指针。

4.并发重映射（Concurrent Remap）- 并发

目标：更新应用线程中所有指向旧 Region 的指针，使其直接指向新地址，消除读屏障的转发开销。

特点：与应用线程并发执行，优先级较低，可被 GC 周期打断（下次 GC 继续处理）。

本质还是标记-复制

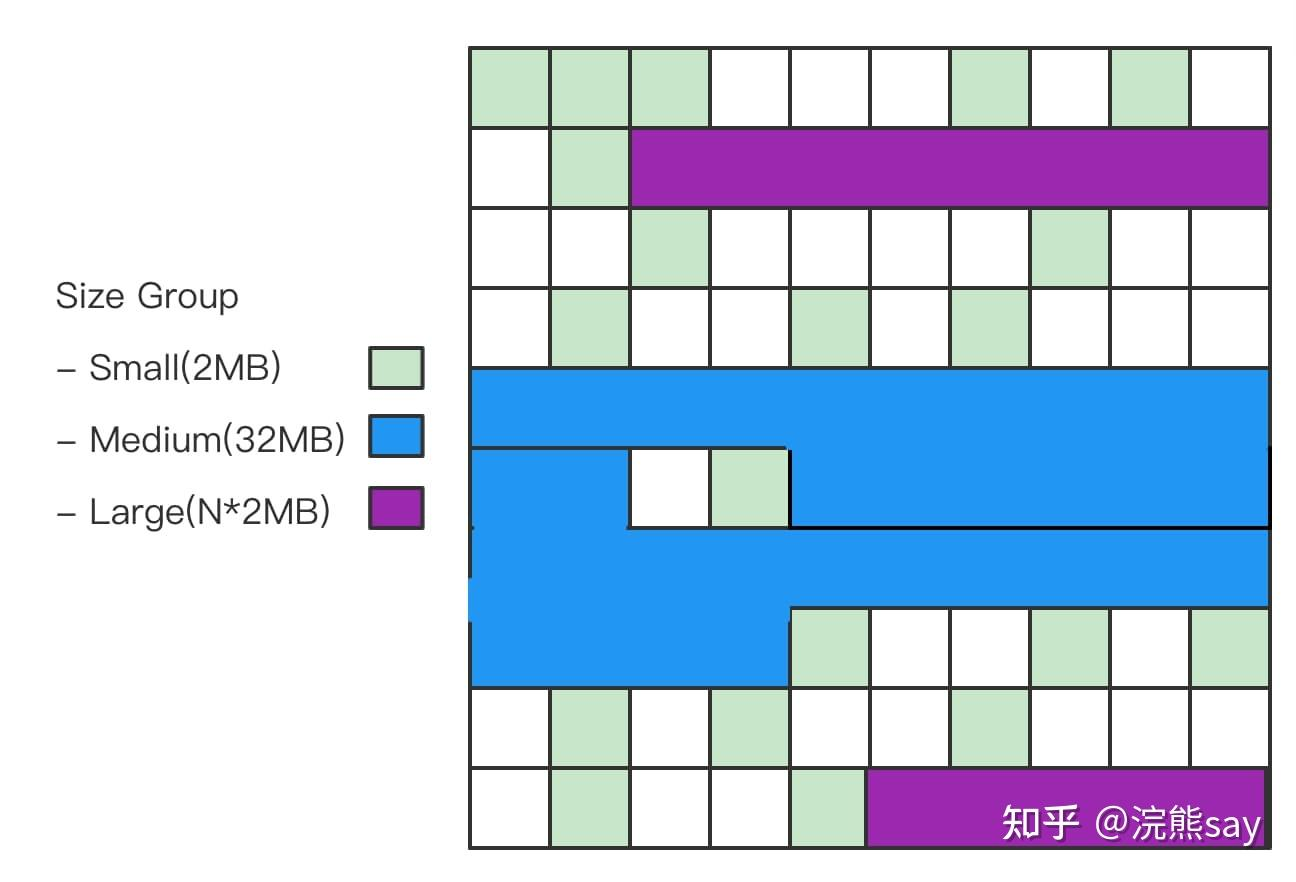
upload successful

动态的区域容量大小：

ZGC引入了不同大小的Region，包括Small Region（2MB）、Medium Region（32MB）和Large Region（可变大小），使得ZGC在内存分配时能够更好地适应不同大小的对象，提高内存利用率。

upload successful

ZGC主要问题

浮动垃圾：无分代导致全堆扫描，新对象需下次GC回收

内存开销：颜色指针和读屏障带来额外开销

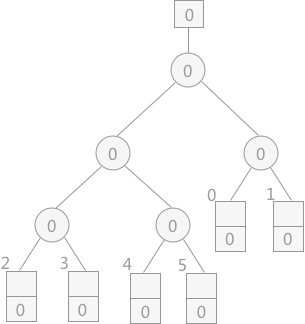
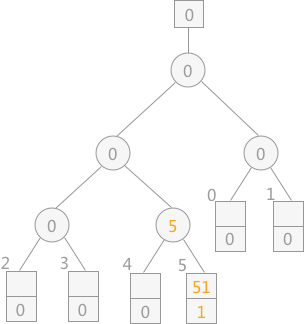
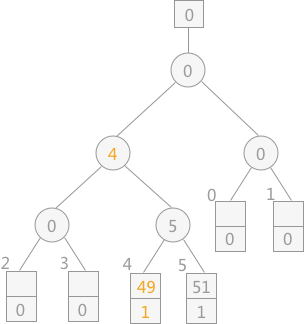
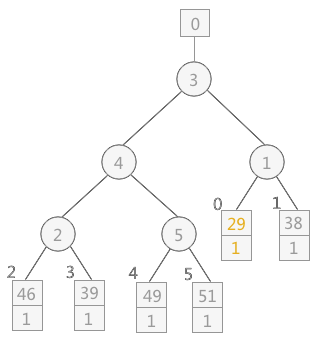
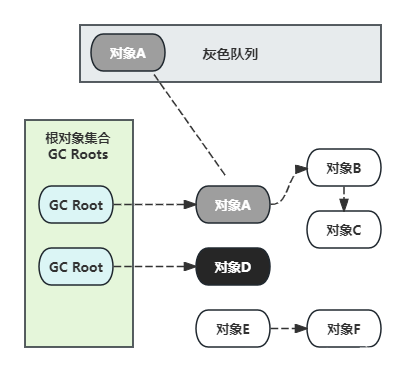
三色标级

CMS和G1都有三色标记算法。标记对象的颜色其实是通过位图（bitmap）实现的，默认的白色对象的bit为0，黑色对象的bit位会被设置为1，而灰色对象不会体现在位图，会被放置于一个单独的队列

upload successful

面试

Full GC

1. 老年代空间不足

这是最常见的触发原因：

新生代对象经过 Minor GC 后，存活对象需要晋升到老年代，但老年代剩余空间不足以容纳这些对象。

大对象直接分配到老年代时，老年代空间不足（大对象指需要连续内存的对象，如大数组、大字符串）。

老年代中内存碎片过多，虽然总空间足够，但没有连续的内存块容纳新的大对象（CMS 收集器尤为明显）。

2. 永久代 / 元空间（Metaspace）不足

JDK 7 及之前：永久代（PermGen）存储类元数据、常量池等，当永久代空间不足时，会触发 Full GC 尝试回收无用的类信息（如卸载不再使用的类），若回收后仍不足则抛出OutOfMemoryError: PermGen space。

JDK 8 及之后：永久代被元空间（Metaspace）取代，元空间默认使用本地内存，但如果设置了-XX:MaxMetaspaceSize且达到上限，也会触发 Full GC 尝试卸载类，失败则抛出OutOfMemoryError: Metaspace。

3. CMS 收集器的特殊触发场景

CMS（Concurrent Mark Sweep）是老年代并发收集器，除了老年代不足外，还有专属触发条件：

CMS Concurrent Mode Failure：CMS 在并发标记 / 清理阶段，老年代空间被新对象占满，无法继续并发回收，会触发 “Concurrent Mode Failure”，进而强制触发 Full GC（通常会退化为 Serial Old 收集器，停顿时间更长）。

CMS 晋升失败（Promotion Failure）：新生代 Minor GC 时，存活对象要晋升到老年代，但老年代空间不足，且 CMS 无法及时腾出空间，触发 Full GC。

显式设置-XX:CMSFullGCsBeforeCompaction：指定 CMS 执行 N 次 Full GC 后，触发一次内存碎片整理（Serial Old），这也是 Full GC 的一种。

4. 显式调用 System.gc ()

代码中调用System.gc()或Runtime.getRuntime().gc()时，JVM可能触发 Full GC（注意：这只是建议，JVM 可通过-XX:+DisableExplicitGC参数禁用该行为）。

常见场景：一些第三方库、框架（如 NIO 的 DirectByteBuffer 回收）可能会调用该方法，导致非预期的 Full GC。

5. G1 收集器的 Full GC 触发

G1（Garbage-First）作为混合收集器，触发 Full GC 的场景包括：

老年代达到-XX:InitiatingHeapOccupancyPercent（默认 45%）阈值，且并发回收无法及时释放空间。
新生代晋升失败、大对象分配失败，且 G1 的混合回收来不及处理。

G1 的回收过程中，记忆集（Remembered Set）维护异常，也可能触发 Full GC。

6. 其他特殊场景

JVM 在做堆内存快照（如 jmap dump）时，可能会触发 Full GC 以获取一致性的内存快照。
某些 JVM 参数配置不当（如新生代 / 老年代比例不合理），也可能间接导致频繁 Full GC。

怎么定位？

查看 GC 日志：添加 JVM 参数打印详细 GC 日志，关键参数：

1	-XX:+PrintGCDetails -XX:+PrintGCDateStamps -Xloggc:/path/to/gc.log

日志中会包含Full GC关键字，以及触发原因（如Allocation Failure、Metadata GC Threshold等）。

使用工具分析：

jstat：jstat -gcutil 1000（每秒打印 GC 统计，关注 O 列（老年代使用率）和 FGCT 列（Full GC 总时间））。

jvisualvm/JMC：可视化监控 GC 状态，定位 Full GC 触发时机。

CMS vs G1

1.堆内存管理：连续分区（G1） vs 离散 Region（CMS）

G1 可以动态调整年轻代 Region 的数量，回收时只挑选 “垃圾多、回收性价比高” 的 Region，从根本上限制单次回收的范围。

2.延迟控制：被动并发 vs 主动预测

范围可控，有预测机制

3.标记清除（CMS） vs 标记复制（G1）

内存碎片

4.stw period

整个 Young GC 全程都是 STW 阶段，但因为只处理年轻代 Region，且多线程并行执行，耗时通常在几毫秒～30 毫秒。

Full GC 会回收整个堆，全程 STW，秒级。

G1_STW

CMS_STW

2025-12-21

多头注意力机制

upload successful

单头注意力

Q（查询query）=> （seq_len×d_k）

K（键值key）=> Q*K 输出每个单词和其他单词的概率关系分布（seq_len x seq_len）

V（值 value）=> 赋予每个向量重要性

upload successful

d_k：是 Q/K 的维度，通常远小于 d_model（如 d_k=64），目的是降低计算复杂度，将原始得分除以 √d_k，避免因 d_k 过大导致 Softmax 输出过于极端（梯度消失）。

d_model：输入词向量的维度。

输入都是同一个词向量+位置编码，注意力的Q、K、V矩阵参数不同但是长宽相同（seq_len×d_k）

Attention = softmax(Q×K^T / √d_k )*V

┌─────────────────────────────────────────────────────────┐
│ 输入X (seq_len×d_model)                                │
└───────────┬───────────┬───────────┬───────────────────┘
            │           │           │
            ▼           ▼           ▼
┌───────────┐   ┌───────────┐   ┌───────────┐
│ W_Q       │   │ W_K       │   │ W_V       │
└───────────┘   └───────────┘   └───────────┘
            │           │           │
            ▼           ▼           ▼
┌───────────┐   ┌───────────┐   ┌───────────┐
│ Q         │   │ K         │   │ V         │
└───────────┘   └───────────┘   └───────────┘
            │           │           │
            └───────────┼───────────┘
                        │
                        ▼
┌─────────────────────────────────────────┐
│ Q×K^T / √d_k → Softmax → 注意力权重    │
└─────────────────────────────────────────┘
                        │
                        ▼
┌─────────────────────────────────────────┐
│ 注意力权重 × V → 单头输出                │
└─────────────────────────────────────────┘
                        │
                        ▼
┌─────────────────────────────────────────┐
│ 多头拼接 → W_O → 最终输出                │
└─────────────────────────────────────────┘

单头注意力的输出是融合了上下文信息的 Token 表示矩阵

多头注意力

并行执行多个单头注意力，然后将结果拼接并线性变换，目的是捕捉不同维度的上下文信息。

原先（d_model）的矩阵分解成h个头，每个头都是单头注意力（d_k），但是拼接起来等于d_model

Q, K, V (seq_len×d_model)
  |
  ├→ 分拆为h个头 → Q1-Qh, K1-Kh, V1-Vh (每个seq_len×d_k)
  |
  ├→ 头1：自注意力 → Output1 (seq_len×d_k)
  ├→ 头2：自注意力 → Output2 (seq_len×d_k)
  ├→ ...
  ├→ 头h：自注意力 → Outputh (seq_len×d_k)
  |
  ├→ 拼接 → Output (seq_len×h*d_k)
  |
  └→ 线性变换W_O → 最终输出 (seq_len×d_model)

掩码自注意力（Masked Self-Attention）

用于 Transformer 的解码器，防止模型看到未来的 Token。
通过在注意力得分矩阵中加入掩码（Mask），将未来 Token 的得分设为 -∞，Softmax 后权重为 0。

2020-05-20

gcc优化

在优化之前要提醒的内容：

1.任何级别的优化都将带来代码结构的改变。例如：对分支的合并和消除，对公用子表达式的消除，对循环内load/store操作的替换和更改等，都将会使目标代码的执行顺序变得面目全非，导致调试信息严重不足。

2.内存操作顺序改变所带来的问题：在O2优化后，编译器会对影响内存操作的执行顺序。例如：-fschedule-insns允许数据处理时先完成其他的指令；-fforce-mem有可能导致内存与寄存器之间的数据产生类似脏数据的不一致等。对于某些依赖内存操作顺序而进行的逻辑，需要做严格的处理后才能进行优化。例如，采用volatile关键字限制变量的操作方式，或者利用barrier迫使cpu严格按照指令序执行的。

表示程序性能的标准：CPE（越小性能越优）延迟界限　吞吐量界限

CPE指数只是针对循环代码而言的（几乎可以说代码性能优化就是对循环的优化），它指处理数据的每个元素所消耗的周期数。之所以使用每个元素的周期数而不是每个循环的周期数来度量，是因为循环次数可能随循环展开的程度不同而变化。

延迟界限：当一系列操作必须按照严格的顺序执行时，处理每个元素所历经的关键路径（最长路径）的周期数。当数据相关问题限制了指令级并行的能力时，延迟界限能够限制程序性能。

吞吐量界限：处理器功能单元全力运行时的原始计算能力。比如处理器具有两个能同时做乘法的单元，对于只有1次乘/元素的循环而言，此时的吞吐量界限就是0.5。吞吐量界限是程序性能的终极界限。

程序转换的优化安全：

内存别名使用：
1
2
3
4
5
6
7
void twiddle1(long*xp,long*yp){
*xp+=*yp;
*xp+=*yp
}
void twiddle2(long*xp,long*yp){
*xp+=2* *yp
}
如果*xp=*yp，则twiddle1会是增加四倍（xp翻倍的同时yp也翻倍），twidde2则是增加三倍，编译器不知道xp会不会等于yp，所以无法将代码从twiddle1优化为twiddle2

2.函数调用合并

long counter=0;
long f(){
    return counter++;
}

long func1(){
    return f()+f()+f()+f();
}

long func2(){
    return 4*f();
}

func1的结果是0+1+2+3=6，而func2的结果是4*0=0

循环展开技术（－O3）

一种牺牲程序的尺寸来加快程序的执行速度的优化方法。可以由程序员完成，也可由编译器自动优化完成。循环展开最常用来降低循环开销，为具有多个功能单元的处理器提供指令级并行。也有利于指令流水线的调度。

// 计算p[i]=a[0]+...a[i]
void psum1(float a[],float p[],long n){
    long i;
    p[0]=a[0];
    for(i=1;i<n;i++){
        p[i]=p[i-1]+a[i]
    }
}

void psum1(float a[],float p[],long n){
    long i;
    p[0]=a[0];
    for(i=1;i<n;i++){
        float mid_val=p[i-1]+a[i];
        p[i]=mid_val;
        p[i+1]=mid_val+a[i+1];
    }
    // 对奇数值的特殊处理
    if(i<n){
        p[i]=p[i-1]+a[i];  
    }
}

upload successful

gcc　参数优化

-Og 使用基本的优化
-O1 … -O3 使用更大量的优化，但是也可能增加程序的规模（主要以O1为主）

// 通过修改data_t修改数据类型
#define data_t int
// 通过修改OP来修改执行的是加还是乘
#define IDENT 0
#define OP +
void combine1(vec_ptr v,data_t *dest){
    long i;
    
    *dest=IDENT;
    for(i=0;i<vec_length(v);i++){
        data_t val;
        get_vec_element(v,i,&val);
        *dest=*dest OP val;
    }
}

upload successful

频繁使用数据缓存（针对全局变量和数组保存中间结果）

// combine1
for(i=0;i<vec_length(v);i++){
    ......
}

// combine2
void combine2(vec_ptr v,data_t *dest){
    long i;
    long length=get_vec_element(v,i,&val);
  
    *dest=IDENT;
    for(i=0;i<length;i++){
        data_t val;
        get_vec_element(v,i,&val);
        *dest=*dest OP val;
    }
}

upload successful

减少过程调用

把函数调用取消直接访问元素，性能没啥提升。

data_t* get_vec_start(vec_ptr v){
        return v->data;
}
// combine3
void combine3(vec_ptr v,data_t *dest){
    long i;
    long length = get_vec_element(v,i,&val);
    data_t *data = get_vec_start(v);

    *dest=IDENT;
    for(i=0;i<length;i++){
        data_t val;
        get_vec_element(v,i,&val);
        *dest=*dest OP data[i];
    }
}

upload successful

使用临时变量替代传入的指针变量（临时变量方便寄存器优化而不是内存地址读取数据）

void combine4(vec_ptr v,data_t *dest){
        long i;
        long length = vec_length(v);
        data_t *data=get_vec_start(v);
        data_t acc=IDENT;

        for(i=0;i<length;i++){
                acc=acc OP data[i];
        }
        *dest=acc;
}

upload successful

k*n循环展开

步长为二，一个循环（21）

void combine5(vec_ptr v,data_t *dest){
        long i;
        long length = vec_length(v);
        long limit = length-1;
        data_t *data=get_vec_start(v);
        data_t acc=IDENT;
        
        // combine 2 elements at a time
        for(i=0;i<limit;i+=2){
                acc=(acc OP data[i])OP data[i+1];
        }
        // Finish any remaining elements
        for(;i<length;i++){
                acc = acc OP data[i];
        }
        *dest=acc;
}

步长为二，两个循环（22）

void combine6(vec_ptr v,data_t *dest){
        long i;
        long length = vec_length(v);
        long limit = length-1;
        data_t *data=get_vec_start(v);
        data_t acc0=IDENT;
        data_t acc1=IDENT;        
        // combine 2 elements at a time
        for(i=0;i<limit;i+=2){
                acc0=(acc0 OP data[i]);
                acc1=(acc1 OP data[i+1]);
        }
        // Finish any remaining elements
        for(;i<length;i++){
                acc0 = acc0 OP data[i];
        }
        *dest=acc0 OP acc1;
}

重新结合变换（k*1a）

void combine7(vec_ptr v,data_t *dest){
        long i;
        long length = vec_length(v);
        long limit = length-1;
        data_t *data=get_vec_start(v);
        data_t acc=IDENT;
        
        // combine 2 elements at a time
        for(i=0;i<limit;i+=2){
                acc=acc OP (data[i] OP data[i+1]);
        }
        // Finish any remaining elements
        for(;i<length;i++){
                acc = acc OP data[i];
        }
        *dest=acc;
}

寄存器溢出

现代ｘ８６架构拥有１６个寄存器，还有１６个ＹＭＭ寄存器可以存储浮点型数，如果需要缓存的变量超过该个数则需要将数据存放到内存，性能可能会下降。

条件控制转移（if…else）　VS　条件传送（ ? … : … ）

条件控制转移指根据代码的条件结果来选择执行的路径，条件传送指先把结果执行，在根据条件结果选择结果值。在相同的情况下，条件传送性能比条件控制转移高。

//  CPE 13.5
void minmax1(long a[],long b[],long n){
    long i;
    for(i=0;i<n;i++){
        long t=a[i];
        a[i]=b[i];
        b[i]=t;
    }
}

// CPE 4.0
void minmax2(long a[],long b[],long n){
    for(i=0;i<n;i++){
        long min=a[i]<b[i]?a[i]:b[i];
        long max=a[i]<b[i]?b[i]:a[i];
        a[i]=min;
        b[i]=max;
    }
}

2020-05-17

const

　作用域：

默认状态下，Const对象仅在文件内有效。所以不同文件的const对象不是同一个对象，即使名字相同，因为这样才能避免重复定义。

那为了使一个非常量表达式的const变量在不同文件之间可以共享，可以使用extern来解决问题。

1	extern const int temp;

两种一样的写法

const int a; int const a; 这两个写法是等同的

const int *a; int const* a;含义相同。

　常量指针和指针常量

常量指针声明：const int * p; int const * p;（指针指向常量）

具有只能够读取内存中数据，却不能够修改内存中数据的属性的指针，称为指向常量的指针。

指针常量声明：int * const p=&a;（指针指向常量地址）

指针常量是指指针所指向的位置不能改变，即指针本身是一个常量，但是指针所指向的内容可以改变。

指针常量必须在声明的同时对其初始化，不允许先声明一个指针常量随后再对其赋值，这和声明一般的常量是一样的。
1
2
3
4
5
6
7
int num=0;

int*const cur=&num;//一直指向num

const double pi=3.1415;

const double * const pip=π//指向常量的常量指针。

2020-05-15

memset与虚函数

class BaseParameters
{
public:
  virtual void reset() {}
};
class MyParameters : public BaseParameters
{
public:
  int data[3];
  int buf[3];
};
MyParameters my_pars;
memset(&my_pars, 0, sizeof(my_pars));
BaseParameters* pars = &my_pars;
//.....
MyParameters* my = dynamic_cast<MyParameters*>(pars);

初始化数据结构MyParameters里的data和buf，正常来说需要初始化的内存空间是sizeof(int) 3 2 = 24字节，但是使用memset初始化MyParameters类型的数据结构时，sizeof(my_pars)却是28字节。

因为为了实现多态机制，C++对有虚函数的对象会包含一个指向虚函数表(V-Table)的指针，当使用memset时，会把该虚函数表的指针也初始化为0，而dynamic_cast也使用RTTI技术，运行时会使用到V-Table，可此时由于与V-Table的链接已经被破坏，导致程序发生异常。

2020-05-15

归并排序为什么要用败者树？

https://www.zhihu.com/question/35144290/answer/148681658

堆排序的时间复杂度跟败者树的时间复杂度一致为什么不用堆？$O(nklog_k(n) + k) =O(nklog_kn)$

其实一开始就是用堆来完成多路归并的，但是人们发现堆每次取出最小值之后，把最后一个数放到堆顶，调整堆的时候，每次都要选出父节点的左右两个孩子节点的最小值，然后再用孩子节点的最小值和父节点进行比较，所以每调整一层需要比较两次。这时人们想能否简化比较过程，这时就有了胜者树。

这样每次比较只用跟自己的兄弟节点进行比较就好，所以用胜者树可以比堆少一半的比较次数。而胜者树在节点上升的时候首先需要获得父节点，然后再获得兄弟节点，然后再比较。这时人们又想能否再次减少比较次数，于是就有了败者树。

在使用败者树的时候，每个新元素上升时，只需要获得父节点并比较即可。所以总的来说，减少了访存的时间。（拿空间换时间）

原因：胜者树以小为胜的话，如果比较兄弟节点发现更小直接替代父节点即可，如果更大则兄弟节点胜出。
败者树比较父节点指向的点发现更大直接替换败者即可，更小则不需要替换然后接着上移。

二者都是顶点缺失，都要从底部叶节点遍历到顶点。

最后就是现在程序的主要瓶颈在于访存了，计算倒几乎可以忽略不计。

2020-05-15

置换-选择排序

http://data.biancheng.net/view/78.html

如果内存为W，则内排序算法最多只能对大小略小于W的段进行排序。置换-选择排序可以降低段的个数

置换—选择排序算法的具体操作过程为：

首先从有24个记录的初始文件中输入 6 个记录到内存工作区中；
从内存工作区中选出关键字最小的记录，将其记为 MINIMAX 记录；
然后将 MINIMAX 记录输出到归并段文件中；
此时内存工作区中还剩余 5 个记录，若初始文件不为空，则从初始文件中输入下一个记录到内存工作区中；
从内存工作区中的所有比 MINIMAX 值大的记录中选出值最小的关键字的记录，作为新的 MINIMAX 记录；
重复过程 3—5，直至在内存工作区中选不出新的 MINIMAX 记录为止，由此就得到了一个初始归并段；
重复 2—6，直至内存工作为空，由此就可以得到全部的初始归并段。

upload successful

具体步骤：

首先输入前 6 个记录到内存工作区，其中关键字最小的为 29，所以选其为 MINIMAX 记录，同时将其输出到归并段文件中，如下图所示：

upload successful

2.此时初始文件不为空，所以从中输入下一个记录 14 到内存工作区中，然后从内存工作区中的比 29 大的记录中，选择一个最小值作为新的 MINIMAX 值输出到归并段文件中，如下图所示：

upload successful

3.初始文件还不为空，所以继续输入 61 到内存工作区中，从内存工作区中的所有关键字比 38 大的记录中，选择一个最小值作为新的 MINIMAX 值输出到归并段文件中，如下图所示：

upload successful

4.如此重复性进行，直至选不出 MINIMAX 值为止，如下图所示：

upload successful

5.当选不出 MINIMAX 值时，表示一个归并段已经生成，则开始下一个归并段的创建，创建过程同第一个归并段一样，这里不再赘述。

败者树的实现：

在不断选择新的 MINIMAX 记录时，为了防止新加入的关键字值小的的影响，每个叶子结点附加一个序号位，当进行关键字的比较时，先比较序号，序号小的为胜者；序号相同的关键字值小的为胜者。

在初期创建败者树时也可以通过不断调整败者树的方式，其中所有记录的序号均设为 0 ，然后从初始文件中逐个输入记录到内存工作区中，自下而上调整败者树。过程如下：

1.首先创建一个空的败者树，如下图所示：

upload successful

2.从初始文件中读入关键字为 51 的记录，自下往上调整败者树，如下图所示：

upload successful

提示：序号 1 默认为比 0 小，为败者。

3.从初始文件中读入关键字为 49 的记录，调整败者树如下图所示：

upload successful

4.从初始文件依次读入关键字为 39、46、38、29 的记录，调整败者树如下图所示：

upload successful

5.由败者树得知，其最终胜者为 29，设为 MINIMAX 值，将其输出到初始归并文件中，同时再读入下一个记录 14，调整败者树，如下图所示：

通过不断地向败者树中读入记录，会产生多个 MINIMAX，直到最终所有叶子结点中的序号都为 2，此时产生的新的 MINIMAX 值的序号 2（循环判定胜者的段号决定是否输出新段），表明此归并段生成完成，而此新的 MINIMAX 值就是下一个归并段中的第一个记录。

注意：当读入新的记录时，如果其值比 MINIMAX 大，其序号则仍为 1；反之则为 2 ，比较时序号大的。

总结：

通过置换选择排序算法得到的初始归并段，其长度并不会受内存容量的限制，且通过证明得知使用该方法所获得的归并段的平均长度为内存工作区大小的两倍。

若不计输入输出的时间，通过置换选择排序生成初始归并段的所需时间为O(nlogw)（其中 n 为记录数，w 为内存工作区的大小）。

以下代码有问题，有时候会多生成几个数，但是可以拿来做个参考。

#include <stdio.h>
#define MAXKEY 10000
#define RUNEND_SYMBOL 10000 // 归并段结束标志
#define w 6     // 内存工作区可容纳的记录个数
#define N 24    // 设文件中含有的记录的数量
typedef int KeyType; // 定义关键字类型为整型

// 记录类型
typedef struct{
    KeyType key; // 关键字项
}RedType;

typedef int LoserTree[w];// 败者树是完全二叉树且不含叶子，可采用顺序存储结构
typedef struct
{
    RedType rec; /* 记录 */
    KeyType key; /* 从记录中抽取的关键字 */
    int rnum; /* 所属归并段的段号 */
}RedNode, WorkArea[w];

// 从wa[q]起到败者树的根比较选择MINIMAX记录，并由q指示它所在的归并段
void Select_MiniMax(LoserTree ls,WorkArea wa,int q){
    int p, s, t;
// ls[t]为q的双亲节点，p作为中介

    for(t = (w+q)/2,p = ls[t]; t > 0;t = t/2,p = ls[t]){
        // 段号小者 或者 段号相等且关键字更小的为胜者
        if(wa[p].rnum < wa[q].rnum || (wa[p].rnum == wa[q].rnum && wa[p].key < wa[q].key)){
            s=q;
            q=ls[t]; //q指示新的胜利者
            ls[t]=s;
        }
    }
    ls[0] = q; // 最后的冠军
}
//输入w个记录到内存工作区wa,建得败者树ls,选出关键字最小的记录，并由s指示其在wa中的位置。
void Construct_Loser(LoserTree ls, WorkArea wa, FILE *fi){
    int i;
    for(i = 0; i < w; ++i){
        wa[i].rnum = wa[i].key = ls[i] = 0;
    }
    for(i = w - 1; i >= 0; --i){
        fread(&wa[i].rec, sizeof(RedType), 1, fi);// 输入一个记录
        wa[i].key = wa[i].rec.key; // 提取关键字
        wa[i].rnum = 1; // 其段号为＂1＂
        Select_MiniMax(ls,wa,i); // 调整败者树
    }
}

// 求得一个初始归并段，fi为输入文件指针，fo为输出文件指针。
void get_run(LoserTree ls,WorkArea wa,int rc,int *rmax,FILE *fi,FILE *fo){
    int q;
    KeyType minimax;
    // 选得的MINIMAX记录属当前段时
    while(wa[ls[0]].rnum == rc){
        q = ls[0];// q指示MINIMAX记录在wa中的位置
        minimax = wa[q].key;
        // 将刚选得的MINIMAX记录写入输出文件
        fwrite(&wa[q].rec, sizeof(RedType), 1, fo);
        // 如果输入文件结束，则虚设一条记录（属＂rmax+1＂段）
        if(feof(fi)){
            wa[q].rnum = *rmax+1;
            wa[q].key = MAXKEY;
        }else{ // 输入文件非空时
            // 从输入文件读入下一记录
            fread(&wa[q].rec,sizeof(RedType),1,fi);
            wa[q].key = wa[q].rec.key;// 提取关键字
            if(wa[q].key < minimax){
                // 新读入的记录比上一轮的最小关键字还小，则它属下一段
                *rmax = rc+1;
                wa[q].rnum = *rmax;
            }else{
                // 新读入的记录大则属当前段
                wa[q].rnum = rc;
            }
        }
        // 选择新的MINIMAX记录
        Select_MiniMax(ls, wa, q);
    }
}

//在败者树ls和内存工作区wa上用置换－选择排序求初始归并段
void Replace_Selection(LoserTree ls, WorkArea wa, FILE *fi, FILE *fo){
    int rc, rmax;
    RedType j;
    j.key = RUNEND_SYMBOL;
    // 初建败者树
    Construct_Loser(ls, wa, fi);
    rc = rmax =1;//rc指示当前生成的初始归并段的段号，rmax指示wa中关键字所属初始归并段的最大段号

    while(rc <= rmax){// ＂rc=rmax+1＂标志输入文件的置换－选择排序已完成
        // 求得一个初始归并段
        get_run(ls, wa, rc, &rmax, fi, fo);
        fwrite(&j,sizeof(RedType),1,fo);//将段结束标志写入输出文件
        rc = wa[ls[0]].rnum;//设置下一段的段号
    }
}

void print(RedType t){
    printf("%d ",t.key);
}

int main(){
    RedType a[N]={51,49,39,46,38,29,14,61,15,30,1,48,52,3,63,27,4,13,89,24,46,58,33,76};
    RedType b;
    FILE *fi,*fo; //输入输出文件
    LoserTree ls; // 败者树
    WorkArea wa; // 内存工作区
    int i, k;
    fo = fopen("ori","wb"); //准备对 ori 文本文件进行写操作
    //将<u>[数组](http://data.biancheng.net/view/181.html)</u> a 写入大文件ori
fwrite(a, sizeof(RedType), N, fo);
    fclose(fo); //关闭指针 fo 表示的文件
    fi = fopen("ori","rb");//准备对 ori 文本文件进行读操作
    printf("文件中的待排序记录为:\n");
    for(i = 1; i <= N; i++){
        // 依次将文件ori的数据读入并赋值给b
        fread(&b,sizeof(RedType),1,fi);
        print(b);
    }
    printf("\n");
    rewind(fi);// 使fi的指针重新返回大文件ori的起始位置，以便重新读入内存，产生有序的子文件。
    fo = fopen("out","wb");
    // 用置换－选择排序求初始归并段
    Replace_Selection(ls, wa, fi, fo);
    fclose(fo);
    fclose(fi);
    fi = fopen("out","rb");
    printf("初始归并段各为:\n");
    do{
        k = fread(&b, sizeof(RedType), 1, fi); //读 fi 指针指向的文件，并将读的记录赋值给 b，整个操作成功与否的结果赋值给 k
        if(k == 1){
            if(b.key ==MAXKEY){//当其值等于最大值时，表明当前初始归并段已经完成
                printf("\n\n");
                continue;
            }
            print(b);
        }
    }while(k == 1);
    return 0;
}

2020-05-15

外部排序

http://data.biancheng.net/view/77.html

多路归并排序：

二路归并排序

五路归并排序

对于外部排序算法来说，影响整体排序效率的因素主要取决于读写外存的次数，即访问外存的次数越多，算法花费的时间就越多，效率就越低。

对于同一个文件来说，对其进行外部排序时访问外存的次数同归并的次数成正比，即归并操作的次数越多，访问外存的次数就越多（每次归并都要加载硬盘上的待归并文件到内存）。

最后一轮归并的时候内存不够怎么办？

在实际归并的过程中，由于内存容量的限制不能满足同时将 2 个归并段全部完整的读入内存进行归并，只能不断地取 2 个归并段中的每一小部分进行归并，通过不断地读数据和向外存写数据，直至 2 个归并段完成归并变为 1 个大的有序文件。

有关段的预处理如何提升算法效率？

对比2-路还有5-路归并排序可以看出，对于 k-路平衡归并中，增加 k 可以减少归并的次数，从而减少外存读写的次数，最终达到提高算法效率的目的。除此之外，一般情况下对于具有 m 个初始归并段进行 k-路平衡归并时，归并的次数为：$s=⌊log_k⁡m ⌋$（其中 s 表示归并次数）

-方法也就以下两个：
（1）增加 k-路平衡归并中的 k 值；（多路平衡归并算法）
（2）减少初始段的数量m / 增加每个归并段的容量（段太大的话内存可能不够）；（置换-选择排序算法）

2020-05-05

成员初始化的顺序

可以看出成员被初始化的顺序和成员初始化表里面的顺序是没有关系的，只和成员的声明顺序有关。

#include <iostream>
using namespace std;
int seti() {cout << "seti" << endl;return 1;}
int setj() {cout << "setj" << endl;return 1;}
class a
{
public:
    a() {cout << "a()~~~~~" << endl;}
};
class b
{
public:
    b():j(setj()),i(seti()) {cout << "b()~~~~~" << endl;}
    int i;
    a ca;
    int j;
};
int main()
{
    b ob;
    return 0;
}

构造函数执行顺序：public里面 int i 先声明，就先构造 i，然后类a ca 声明，再构造 ca，然后声明 j，就构造 j，最后执行 b() 构造函数里面的东西。

upload successful

另外举个例子：

#include <iostream>
using namespace std;
class A
{
private:
	int n1;
	int n2;
public:
	A():n2(0),n1(n2+2){}
	void Print(){
		cout << "n1:" << n1 << ", n2: " << n2 <<endl;  
	}
};
int main()
{ 
	A a;
	a.Print();
	return 1;
}

因为private里面先定义的n1再定义的n2，但是n1需要n2，n2没有初始化，所以n2是乱码，n1是0。

upload successful

2019-10-14

拉格朗日乘子法和（对偶性与KKT条件）

https://blog.csdn.net/weixin_37688445/article/details/79275526
https://www.matongxue.com/madocs/939.html
https://www.matongxue.com/madocs/987/

拉格朗日乘子法（约束条件为等式）

$\begin{cases}
min f(x) \\
\
h_i(x)=0，i=0，1，…，n
\end{cases}$

在两个图线外相切的时候达到最小值，法向量方向相反

$\begin{cases}
\nabla f(x)=-\nabla \lambda\star h_i(x) => \nabla f(x)+\nabla \lambda\star h_i(x)=0\\
\
h_i(x)=0，i=0，1，…，n
\end{cases}$

最终表达式：

$\begin{cases}
L(x,a)=min[f(x)+\sum_{i=1}^{n}a_ih_i(x)]
\\
h_i(x)=0，i=0，1，…，n
\end{cases}$

求解：$\nabla_xL(x,a)=0$还有$\nabla_aL(x,a)=0$可得最优解的x和a

upload successful

拉格朗日的KKT条件

初试条件：

$\begin{cases}
min f(x) \\
\
g(x) <= 0
\end{cases}$

推导出来的最终公式：

$\begin{cases}
式1： L(x,a)=min[f(x)+\lambda*g(x)]\\
式2： g(x) = 0 \\
式3：\lambda>0
\end{cases}$

*情况1：如果可行解直接落在约束条件范围内，即落在g(x)<0的范围内，则直接删掉约束条件即可。（但是最优点依旧满足前提：公式1即使两条线在$r_f$≈0的时候不相交）

*情况2：如果可行解落在约束条件外，则最优解在边界上去的，即在g(x)=0的曲线上取得。（此时转换为前面讲的等式条件下求最优解的问题，直接套上面的公式）

upload successful

以上两种状况要么落在约束区域内，则$\lambda解$=0，因为直接去掉约束条件即可，要么落在约束条件边界上，则$g(x)解=0$, 综合起来就是$\lambda*g(x)=0$

还有一个问题就是$\lambda$的取值问题，当$\lambda$不等于0的时候，即最优解在$g(x)=0$上取得时，$f(x,y)$梯度方向必须要和$g(x)=0$的梯度方向相反，即$-\nabla_xf(x)=\lambda\nabla_xg(x)$，所以$\lambda$一定大于0，要不然就恒非零了。

upload successful

拉格朗日对偶性：（$\lambda$改为a表示）

1.原始最优化问题：

$\begin{cases}
式1： \min_{x \in R^n} f(x)\\
式2： c_i(x)<=0 ， i=1，2，…，k \\
式3：h_j(x)=0 ，j=1，2，…，l
\end{cases}$

$L(x,a,\beta)=f(x)+\sum{i=1}^{k}a_ic_i(x)+\sum{j=1}^{l}\beta_jh_j(x)$

2.极小极大问题：

$令\thetaP(x)=\max{a,\beta:a_i>=0}L(x,a,\beta)$

如果$i$和$j$当中有一个不满足式2/式3条件，那么必然存在某个$i$满足$c_i(x)>0$，可令$a_i->+\infty$，或者存在某个$j$满足$h_j(x) \ne 0$，则可令$\beta_jh_j(x)\rightarrow +\infty$，而将其余各个$a_i$，$\beta_j$均取为$0$，使得$\theta_P(x)=+\infty$

所以max化的拉格朗日函数 $\theta_P(x)=\begin{cases}
f(x) ， x满足原始问题约束\\
+\infty ，其他
\end{cases}$

接着考虑max条件下的min最优值：

$p^*=min \theta_P(x)=\min_{x} \max_{a,\beta:a_i>=0} L(x,a,\beta)$

3.极大极小问题：

$\max{a,\beta}\theta_D(a,\beta)=\max{a,\beta}\min_{x}L(x,a,\beta)，a_i>=0$

最优解：$d^*=\max_{a,\beta:a_i>=0}\theta_D(a,\beta)$

4.极大极小问题与极小极大问题的解什么时候相等？

maxmin和minmax的最优解有以下大小关系：

$d^*=\max_{a,\beta:a_i>=0}\min_{x}L(x,a,\beta)<=\min_{x} \max_{a,\beta:a_i>=0} L(x,a,\beta)=p^*$

如果满足$f(x)$和$c_i(x)$是凸函数，$h_j(x)$是仿射函数，和KKT条件，则：

$d^*=L(x^*,a^*,\beta^*)=p^*$

KKT条件是$d^\star$ = $p^\star$的充要条件：

$\nabla_xL(x^*,a^*,\beta^*)=0$ $a_i^*c_i(x^*)=0，i=1,2,...,k$ $c_i(x^*)<=0 ，i=1,2,...,k$ $a_i^*>=0 ， i=1,2,...,k$ $h_j(x^*)=0，j=1，...，l$

知识概念

CMS垃圾回收

G1（Garbage First GC）

ZGC

三色标级

面试

Full GC

1. 老年代空间不足

2. 永久代 / 元空间（Metaspace）不足

3. CMS 收集器的特殊触发场景

4. 显式调用 System.gc ()

5. G1 收集器的 Full GC 触发

6. 其他特殊场景

怎么定位？

CMS vs G1

单头注意力

多头注意力

作用域：

1extern const int temp;

两种一样的写法

常量指针和指针常量

　作用域：

1
extern const int temp;

　常量指针和指针常量